α-Rank

OpenSpiel now supports using Alpha-Rank (“α-Rank: Multi-Agent Evaluation by Evolution”, 2019) for both single-population (symmetric) and multi-population games. Specifically, games can be specified via payoff tables (or tensors for the >2 players case) as well as Heuristic Payoff Tables (HPTs).

The following presents several typical use cases for Alpha-Rank. For an example complete python script, refer to open_spiel/python/egt/examples/alpharank_example.py.

Importing the Alpha-Rank module

from open_spiel.python.egt import alpharank
from open_spiel.python.egt import alpharank_visualizer

Running Alpha-Rank on various games

Example: symmetric 2-player game rankings

In this example, we run Alpha-Rank on a symmetric 2-player game (Rock-Paper-Scissors), computing and outputting the rankings in a tabular format. We demonstrate also the conversion of standard payoff tables to Heuristic Payoff Tables (HPTs), as both are supported by the ranking code.

# Load the game
game = pyspiel.load_matrix_game("matrix_rps")
payoff_tables = utils.game_payoffs_array(game)

# Convert to heuristic payoff tables
payoff_tables= [heuristic_payoff_table.from_matrix_game(payoff_tables[0]),
                heuristic_payoff_table.from_matrix_game(payoff_tables[1].T)]

# Check if the game is symmetric (i.e., players have identical strategy sets
# and payoff tables) and return only a single-player’s payoff table if so.
# This ensures Alpha-Rank automatically computes rankings based on the
# single-population dynamics.
_, payoff_tables = utils.is_symmetric_matrix_game(payoff_tables)

# Compute Alpha-Rank
(rhos, rho_m, pi, num_profiles, num_strats_per_population) = alpharank.compute(
    payoff_tables, alpha=1e2)

# Report results
alpharank.print_results(payoff_tables, payoffs_are_hpt_format, pi=pi)

Output

Agent        Rank         Score
-----        ----         -----
0            1            0.33
1            1            0.33
2            1            0.33

Example: multi-population game rankings

The next example demonstrates computing Alpha-Rank on an asymmetric 3-player meta-game, constructed by computing payoffs for Kuhn poker agents trained via extensive-form fictitious play (XFP). Here we use a helper function, compute_and_report_alpharank, which internally conducts the pre-processing and visualization shown in the previous example.

# Load the game
payoff_tables = alpharank_example.get_kuhn_poker_data(num_players=3)

# Helper function for computing & reporting Alpha-Rank outputs
alpharank.compute_and_report_alpharank(payoff_tables, alpha=1e2)

Output

Agent        Rank         Score
-----        ----         -----
(2,3,3)      1            0.22
(3,3,3)      2            0.14
(3,2,3)      3            0.12
(2,2,3)      4            0.09
(3,1,3)      5            0.08
(2,1,3)      6            0.05
(1,2,3)      7            0.04
(2,3,1)      8            0.02
...          ...          ...

Visualizing and reporting results

This section provides details on various methods used for reporting the final Alpha-Rank results.

Basic Ranking Outputs

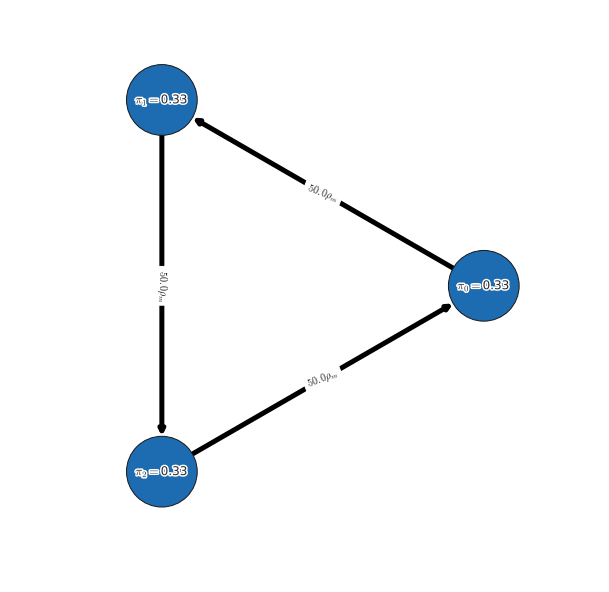
The final rankings computed can be printed in a tabular manner using the following interface:

alpharank.print_results(payoff_tables, payoffs_are_hpt_format, pi=pi)

Output

Agent        Rank         Score
-----        ----         -----
0            1            0.33
1            1            0.33
2            1            0.33

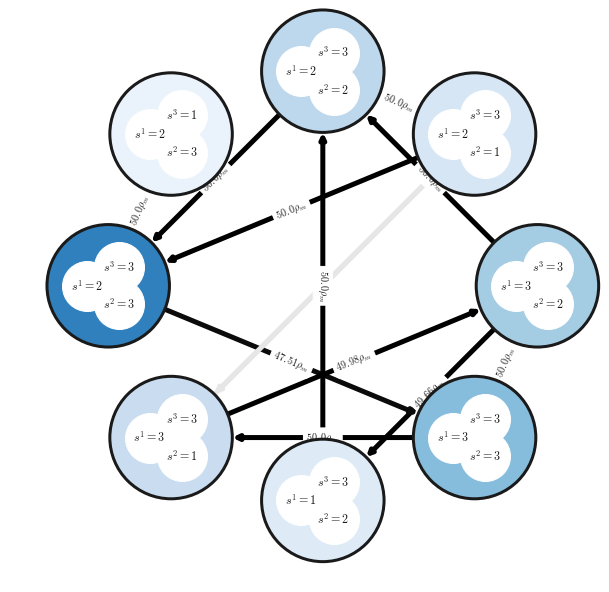
Markov Chain Visualization

One may visualize the Alpha-Rank Markov transition matrix as follows:

m_network_plotter = alpharank_visualizer.NetworkPlot(payoff_tables, rhos,
                                                     rho_m, pi,strat_labels,
                                                     num_top_profiles=8)
m_network_plotter.compute_and_draw_network()

Output

Alpha-sweep plots

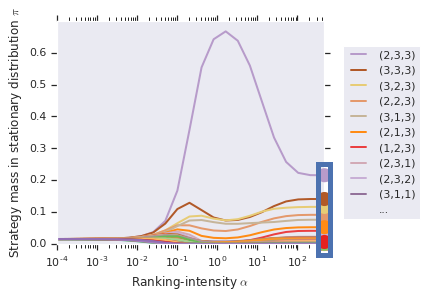
One may choose to conduct a sweep over the ranking-intensity parameter, alpha (as opposed to choosing a fixed alpha). This is, in general, useful for general games where bounds on payoffs may be unknown, and where the ranking computed by Alpha-Rank should use a sufficiently high value of alpha (to ensure correspondence to the underlying Markov-Conley chain solution concept). In such cases, the following interface can be used to both visualize the sweep and obtain the final rankings computed:

alpharank.sweep_pi_vs_alpha(payoff_tables, visualize=True)

Output